带纯滞后的惯性环节
响应曲线法:是一种时域法辨识对象的动态特的方法
大多数工业过程的机理模型是很难建立的,只有采用实验建模。实际建模时,不用过于精确,一般将对象近似为带纯滞后的惯性环节,便于控制。
阶跃响应和矩形脉冲响应
阶跃响应:实验时往往会对正常生产造成影响。
矩形脉冲响应:对正常生产影响小
转换的思路:将矩形脉冲看成正负两个等幅的阶跃信号的叠加,据此而得到输出的阶跃响应。
已知矩形脉冲响应,可以转化为阶跃响应,并进一步利用阶跃响应曲线进行分析。
为矩形脉冲响应 为阶跃响应
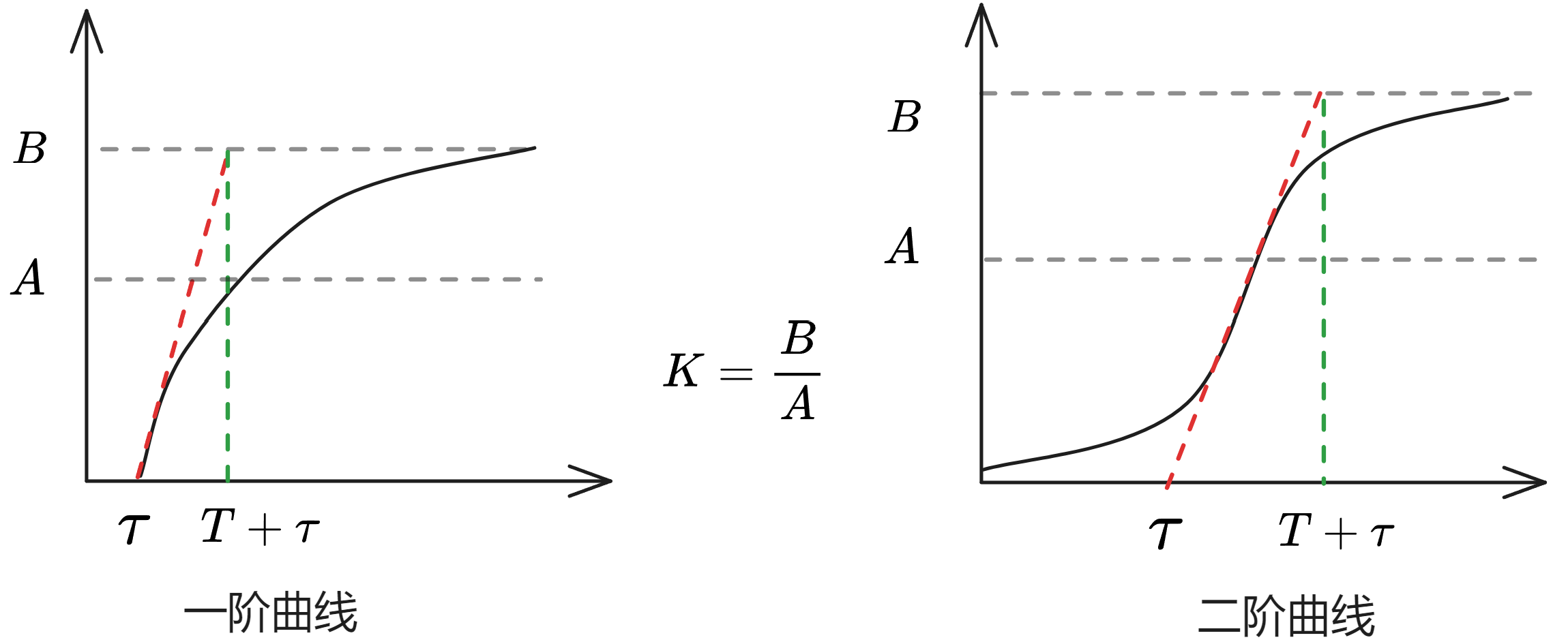
一阶阶跃响应曲线
假设输入信号为
放大倍数/开环增益 时间常数 延迟时间
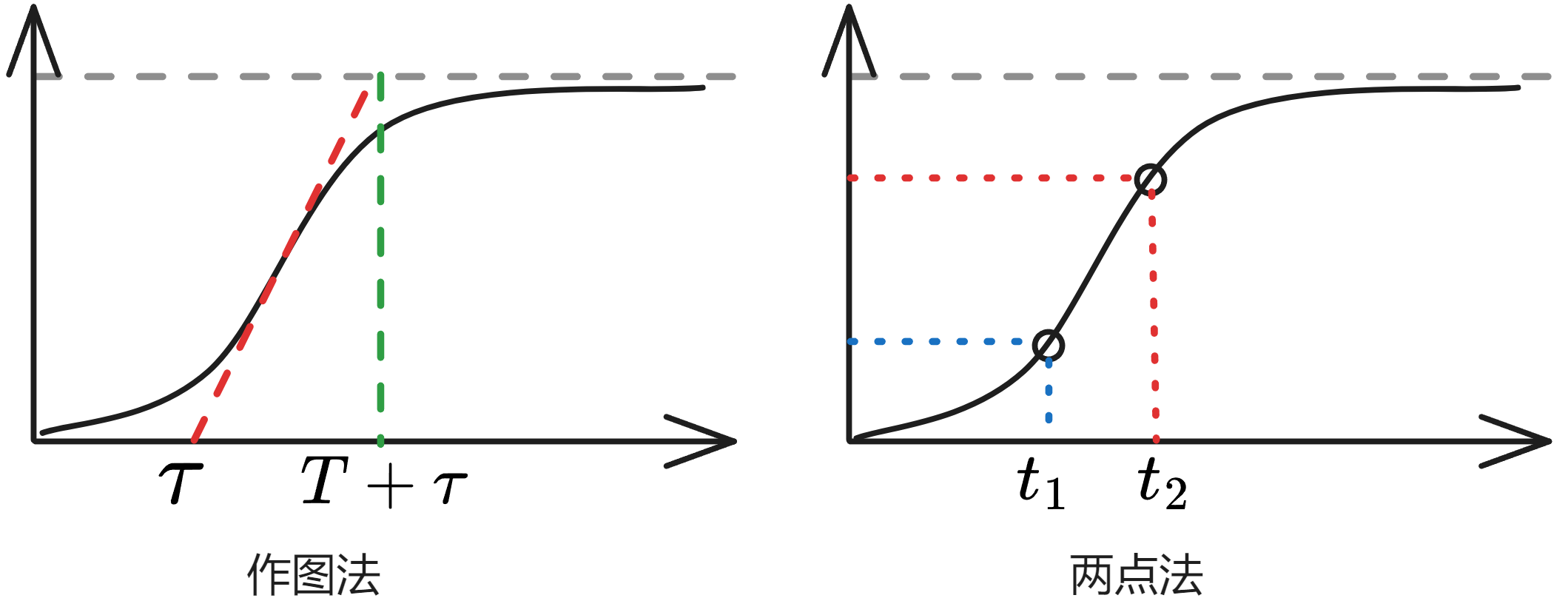
作图法
作切线,直接得到延迟时间和时间常数
两点法
选择两点进行计算
代入任意两点求解
一阶曲线与二阶曲线